The
Pythagorean Theorem
by Dexter Wright
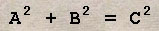
If we consider a field of points arranged in regular rows
and columns it is evident that four of the points determine a square (fig.
1), which we may take as the unit of measurement for areas. But four
squares also meet at a point, (fig. 2). Hence a point at the corner of any
square belongs equally to four squares.
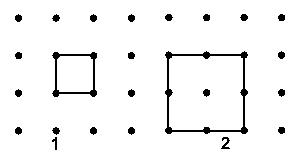
With this in mind, we may say that the point value of
square (1) is one. Since it has four points at each corner, and each
corner belongs to four other squares, only one fourth of each corner
belongs to square (1). ¼ x 4 = 1.
The result obtained by counting points is the same as
that arrived at by calculating the number of square units enclosed by the
points.
Hence, if we wish to measure the area of any square we
can take the number of points it encloses, count these as one each, and
take one-fourth of the number of points at its corners.
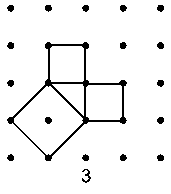
Now draw a diagonal square as shown in figure 3. It
contains one point in the center, and the four corners count for one point
more; hence its point value is 2. The value is the measure of its area -
the size of this square being two of the unit squares. Looking now at the
sides of this figure we see that there is a unit square on each of them -
the two squares contain no points, but have four corner points each, which
gives the point value of each as one point.
Hence we see that the square on the diagonal is equal to
the squares on the two sides; or as it is generally expressed, the square
on the hypotenuse is equal to the sum of the squares on the sides.
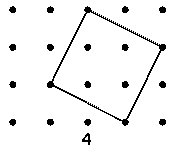
Noticing this fact we proceed to ask if it is always
true. Drawing the square shown in figure 4, we count the number of its
points. There are five altogether. There are four points inside the
diagonal square, and, with the four points at its corners, the point value
is 5 - that is, 5 units of area. And the squares on the sides are
respectively of the area 4 and 1.
Hence in this case also the square on the diagonal is
equal to the sum of the square on the sides.
Iamblicus writes "... he [Pythagoras] was taken captive
by the soldiers of Cambyses, and carried off to Babylon [from Egypt]. Here
he was overjoyed to be associated with the Magi, who instructed him in
their venerable knowledge, and in the most perfect worship of the Gods.
Through their assistance, likewise, he studied and completed arithmetic,
music, and all the other sciences."
And so it is that the right triangle comes down to us as
a symbol of our fourth cardinal virtue. Out of the unequal, indefinite and
unsymmetrical affairs of men comes the equality, definiteness and symmetry
of justice exemplified in the right triangle as having an infinite
diversity of adjustments of its unequal parts [length of sides], and yet
having equal powers [the square on the hypotenuse is equal to the sum of
the squares on the other sides].
back to top | ![]()








